Классификация систем автоматического управления
1.4.1. Классификация по виду математического описания
По виду математического описания (уравнений динамики и статики) системы автоматического управления (САУ) подразделяются на линейные и нелинейные системы (САУ или САР).
Каждый “подкласс” (линейных и нелинейных) подразделяется на еще ряд “подклассов”. Например, линейные САУ (САР) имеют различия по виду математического описания.
Поскольку в этом семестре будут рассматриваться динамические свойства только линейных систем автоматического управления (регулирования), то ниже приведем классификацию по виду математического описания для линейных САУ (САР):
1) Линейные системы автоматического управления, описываемые в переменных «вход-выход» обыкновенными дифференциальными уравнениями (ОДУ) с постоянными коэффициентами:
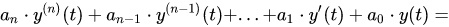
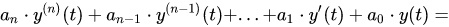
где x(t) – входное воздействие; y(t) – выходное воздействие (регулируемая величина).
Если использовать операторную («компактную») форму записи линейного ОДУ, то уравнение (1.4.1) можно представить в следующем виде:
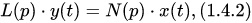
где, p = d/dt — оператор дифференцирования; L(p), N(p) — соответствующие линейные дифференциальные операторы, которые равны:
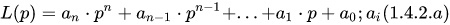
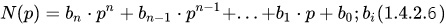
2) Линейные системы автоматического управления, описываемые линейными обыкновенными дифференциальными уравнениями (ОДУ) с переменными (во времени) коэффициентами:
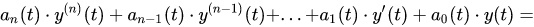
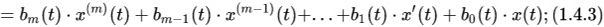
В общем случае такие системы можно отнести и к классу нелинейных САУ (САР).
3) Линейные системы автоматического управления, описываемые линейными разностными уравнениями:
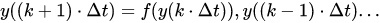
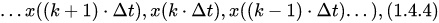
где f(…) – линейная функция аргументов; k = 1, 2, 3… — целые числа; ?t – интервал квантования (интервал дискретизации).
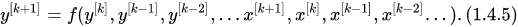
Уравнение (1.4.4) можно представить в «компактной» форме записи:
Обычно такое описание линейных САУ (САР) используется в цифровых системах управления (с использованием ЭВМ).
4) Линейные системы автоматического управления с запаздыванием:
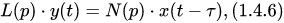
где L(p), N(p) — линейные дифференциальные операторы; ? — время запаздывания или постоянная запаздывания.
Если операторы L(p) и N(p) вырождаются (L(p) = 1; N(p) = 1), то уравнение (1.4.6) соответствует математическому описанию динамики звена идеального запаздывания:
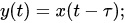
а графическая иллюстрация его свойств привдена на рис. 1.4.1
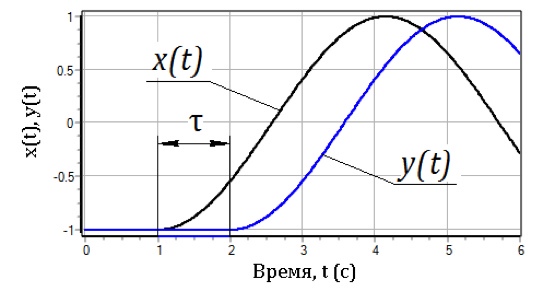
Рис. 1.4.1 — Графики входа и выхода звена идеального запаздывания
5) Линейные системы автоматического управления, описываемые линейными дифференциальными уравнения в частных производных. Нередко такие САУ называют распределенными системами управления. ==> «Абстрактный» пример такого описания:
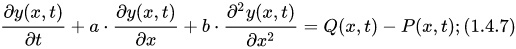
Система уравнений (1.4.7) описывает динамику линейно распределенной САУ, т.е. регулируемая величина зависит не только от времени, но и от одной пространственной координаты.
Если система управления представляет собой «пространственный» объект, то ==>
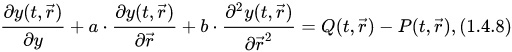
где
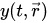
зависит от времени и пространственных координат, определяемых радиусом-вектором
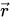
6) САУ, описываемые системами ОДУ, или системами разностных уравнений, или системами уравнений в частных производных ==> и так далее…
Аналогичную классификацию можно предложить и для нелинейных САУ (САР)…
Для линейных систем выполеняются следующие требования:
- линейность статической характеристики САУ;
- линейность уравнения динамики, т.е. переменные в уравнение динамики входят только в линейной комбинации.
Статической характеристикой называется зависимость выхода от величины входного воздействия в установившемся режиме (когда все переходные процессы затухли).
Для систем, описываемых линейными обыкновенными дифференциальными уравнениями с постоянными коэффициентами статическая характеристика получается из уравнения динамики (1.4.1) приравниванием нулю всех нестационарных членов ==>
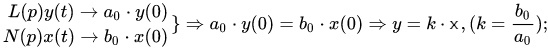
На рис.1.4.2 представлены примеры линейной и нелинейных статических характеристик систем автоматического управления (регулирования).
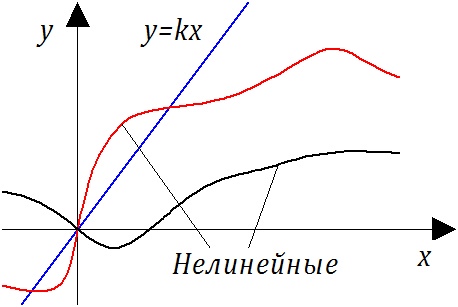
Рис. 1.4.2 — Примеры статических линейных и нелинейных характеристик
Нелинейность членов, содержащих производные по времени в уравнениях динамики, может возникнуть при использовании нелинейных математических операций (*, /, , , sin, ln и т.д.). Например, рассматривая уравнение динамики некоторой «абстрактной» САУ
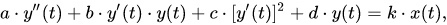
отметим, что в этом уравнении при линейной статической характеристики
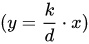
второе и третье слагаемые (динамические члены) в левой части уравнения — нелинейные, поэтому САУ, описываемая подобным уравнением, является нелинейной в динамическом плане.
1.4.2. Классификация по характеру передаваемых сигналов
По характеру передаваемых сигналов системы автоматического управления (или регулирования) подразделяются:
- непрерывные системы (системы непрерывного действия);
- релейные системы (системы релейного действия);
- системы дискретного действия (импульсные и цифровые).
Системой непрерывного действия называется такая САУ, в каждом из звеньев которой непрерывному изменению входного сигнала во времени соответствует непрерывное изменение выходного сигнала, при этом закон изменения выходного сигнала может быть произвольным. Чтобы САУ была непрерывной, необходимо, чтобы статические характеристики всех звеньев были непрерывными.
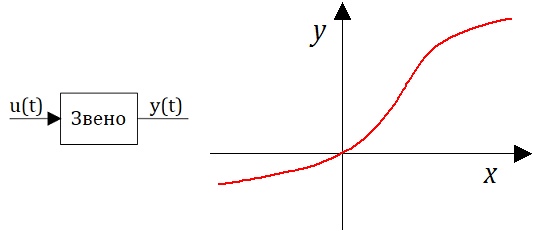
Рис. 1.4.3 — Пример непрерывной системы
Системой релейного действия называется САУ, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина в некоторые моменты процесса управления меняется “скачком” в зависимости от величины входного сигнала. Статическая характеристика такого звена имеет точки разрыва или излома с разрывом.
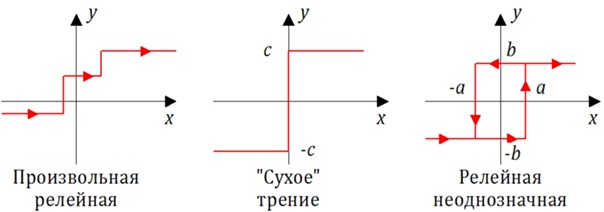
Рис. 1.4.4 — Примеры релейных статических характеристик
Системой дискретного действия называется система, в которой хотя бы в одном звене при непрерывном изменении входной величины выходная величина имеет вид отдельных импульсов, появляющиеся через некоторый промежуток времени.
Звено, преобразующее непрерывный сигнал в дискретный сигнал, называется импульсным. Подобный вид передаваемых сигналов имеет место в САУ с ЭВМ или контроллером.
Наиболее часто реализуются следующие методы (алгоритмы) преобразования непрерывного входного сигнала в импульсный выходной сигнал:
- амплитудно-импульсная модуляция (АИМ);
- широтно-импульсная модуляция (ШИМ).
На рис. 1.4.5 представлена графическая иллюстрация алгоритма амплитудно-импульсной модуляции (АИМ). В верхней части рис. представлена временная зависимость x(t) — сигнала на входе в импульсное звено. Выходной сигнал импульсного блока (звена) y(t) – последовательность прямоугольных импульсов, появляющихся с постоянным периодом квантования ?t (см. нижнюю часть рис.). Длительность импульсов – одинакова и равна ?. Амплитуда импульса на выходе блока пропорциональна соответствующей величине непрерывного сигнала x(t) на входе данного блока.
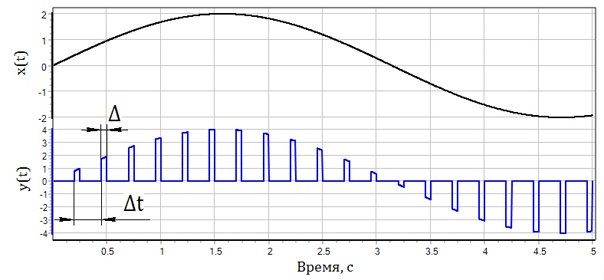
Рис. 1.4.5 — Реализация амплитудно-импульсной модуляции
Данный метод импульсной модуляции был весьма распространен в электронно-измерительной аппаратуре систем управления и защиты (СУЗ) ядерных энергетических установок (ЯЭУ) в 70-х…80-х годах прошлого столетия.
На рис. 1.4.6 представлена графическая иллюстрация алгоритма широтно-импульсной модуляции (ШИМ). В верхней части рис. 1.14 представлена временная зависимость x(t) – сигнала на входе в импульсное звено. Выходной сигнал импульсного блока (звена) y(t) – последовательность прямоугольных импульсов, появляющихся с постоянным периодом квантования ?t (см. нижнюю часть рис. 1.14). Амплитуда всех импульсов – одинакова. Длительность импульса ?t на выходе блока пропорциональна соответствующей величине непрерывного сигнала x(t) на входе импульсного блока.
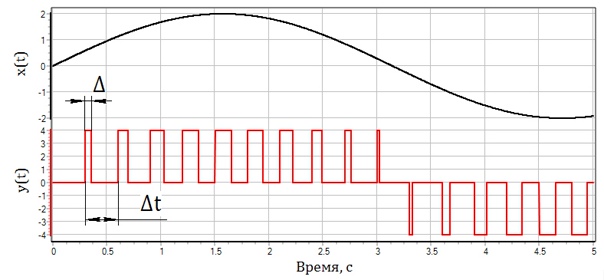
Рис. 1.4.6 — Реализация широтно-импульсной модуляции
Данный метод импульсной модуляции в настоящее время является наиболее распространенным в электронно-измерительной аппаратуре систем управления и защиты (СУЗ) ядерных энергетических установок (ЯЭУ) и САУ других технических систем.
Завершая данный подраздел, необходимо заметить, что если характерные постоянные времени в других звеньях САУ (САР) существенно больше ?t (на порядки), то импульсная система может считаться непрерывной системой автоматического управления (при использовании как АИМ, так и ШИМ).
1.4.3. Классификация по характеру управления
По характеру процессов управления системы автоматического управления подразделяются на следующие типы:
- детерминированные САУ, в которых входному сигналу однозначно может быть поставлен в соответствие выходной сигнал (и наоборот);
- стохастические САУ (статистические, вероятностные), в которых на данный входной сигнал САУ “отвечает” случайным (стохастическим) выходным сигналом.
Выходной стохастический сигнал характеризуется:
- законом распределения;
- математическим ожиданием (средним значением);
- дисперсией (среднеквадратичным отклонением).
Стохастичность характера процесса управления обычно наблюдается в существенно нелинейных САР как с точки зрения статической характеристики, так и с точки зрения (даже в большей степени) нелинейности динамических членов в уравнениях динамики.
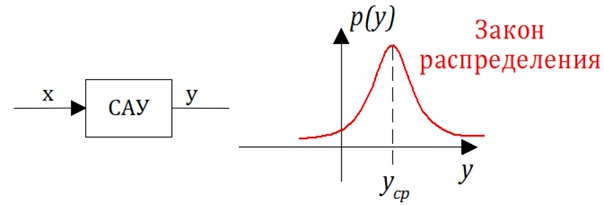
Рис. 1.4.7 — Распределение выходной величины стохастической САУ
Кроме приведенных основных видов классификации систем управления, существуют и другие классификации. Например, классификация может проводиться по методу управления и основываться на взаимодействии с внешней средой и возможности адаптации САУ к изменению параметров окружающей среды. Системы делятся на два больших класса:
1) Обыкновенные (несамонастраивающиеся) СУ без адаптации; эти системы относятся к разряду простых, не изменяющих свою структуру в процессе управления. Они наиболее разработаны и широко применяются. Обыкновенные СУ подразделяются на три подкласса: разомкнутые, замкнутые и комбинированные системы управления.
2) Самонастраивающиеся (адаптивные) СУ. В этих системах при изменении внешних условий или характеристик объекта регулирования происходит автоматическое (заранее не заданное) изменение параметров управляющего устройства за счет изменения коэффициентов СУ, структуры СУ или даже введения новых элементов.
Другой пример классификации: по иерархическому признаку (одноуровневые, двухуровневые, многоуровневые).
Источник:
https://habr.com/ru/post/503820/
Источник: m.vk.com




