Основные понятия теории автоматического управления. Классификация систем автоматического управления.
ОБЩИЕ ПОНЯТИЯ
Теория автоматического управления (ТАУ) появилась во второй половине 19 века сначала как теория регулирования. Широкое применение паровых машин вызвало потребность в регуляторах, то есть в специальных устройствах, поддерживающих устойчивый режим работы паровой машины. Это дало начало научным исследованиям в области управления техническими объектами. Оказалось, что результаты и выводы данной теории могут быть применимы к управлению объектами различной природы с различными принципами действия. В настоящее время сфера ее влияния расширилась на анализ динамики таких систем, как экономические, социальные и т.п. Поэтому прежнее название «Теория автоматического регулирования» заменено на более широкое – «Теория автоматического управления».
Управление каким-либо объектом (объект управления будем обозначать ОУ) есть воздействие на него в целях достижения требуемых состояний или процессов. В качестве ОУ может служить самолет, станок, электродвигатель и т.п. Управление объектом с помощью технических средств без участия человека называется автоматическим управлением. Совокупность ОУ и средств автоматического управления называется системой автоматического управления (САУ).
Основной задачей автоматического управления является поддержание определенного закона изменения одной или нескольких физических величин, характеризующих процессы, протекающие в ОУ, без непосредственного участия человека. Эти величины называются управляемыми величинами. Если в качестве ОУ рассматривается хлебопекарная печь, то управляемой величиной будет температура, которая должна изменяться по заданной программе в соответствии с требованиями технологического процесса.
Самосохранение объектов живой природы является одним из основных свойств, лежащих в основе жизненных явлений. «Сохраняются только такие составляющие живой природы, в которых стремление к самосохранению выражено достаточно ярко», – писал А. А. Ляпунов.
Понятие самосохранения имеет в применении к биологическим системам два аспекта. Прежде всего самосохранение биологическим системам означает ее способность поддерживать в изменяющихся условиях функционирования и окружающей среды стационарное неравновесное состояние, т. е. обеспечивать энтропийный баланс в системе и баланс вещества и энергии. Другой, не менее важный аспект сохранительных свойств биосистем связан с поддержанием гомеостаза – постоянства существенных для жизнедеятельности системы переменных при наличии возмущений во внешней среде.
Живые системы – это необычайно сложные формы, возникшие в результате долгого эволюционного процесса, с сильно выраженными способностями к адаптации, приспособлению и эволюции, обладающие иерархической структурой и представляющие собой интеграцию многих гетерогенных элементов и подсистем. Здесь мы будем касаться далеко не всех вопросов, связанных со сложностью, иерархией, гомеостазом и адаптацией живых систем, ограничиваясь в основном лишь теми их сторонами, где современные методы теории управления позволяют понять или уточнить механизмы функционирования биосистем, выяснить, как образуются определенные свойства в биологических структурах, дать количественные методы и критерии их оценки.
Здесь следует заметить, что конкретные методы классической теории управления, связанные, например, с анализом передаточных функций, не всегда дают адекватное описание сложных биологических и биотехнических систем. Будучи приспособленными для решения относительно простых задач регулирования со сравнительно небольшим числом управляемых переменных, эти методы подчас малоприменимы для исследования биологических проблем, где даже при грубом упрощении приходится иметь дело с десятками и сотнями переменных и параметров. Таковы, например, задачи анализа биохимических или экологических систем, где рассматривается взаимодействие сотен компонент – различных веществ, участвующих в биохимических реакциях, или видов растений и животных, образующих экологические системы. Несколько проще дело обстоит с анализом систем физиологического уровня, где для описания функционирования таких систем, как терморегуляция, регуляция кислородного режима, требуется обычно не более двух-трех десятков переменных.
Поэтому, хотя процессы управления в живых системах в своей основе имеют много общего с управлением в технических системах, сами конкретные методы классической теории управления должны применяться для анализа биосистем с большой осторожностью. Так, использование простой следящей системы в качестве модели гомеостаза в физиологических системах не позволяет дать сколько-нибудь полной картины процессов адаптации и приспособления. Применение такой простой модели для моделирования процессов в нервной системе может дать описание только самой элементарной ее функции – функции слежения у человека-оператора, и непригодно для описания других ее свойств. Можно ожидать, что новые методы, разработанные в теории управления, в ряде случаев будут более адекватным аппаратом исследования биосистем. В частности, применение метода пространства состояний, разработанного в теории управления в последние годы, позволяет по-новому осветить вопросы гомеостаза в физиологических системах.
Основными элементами системы автоматического регулирования являются объект и регулирующее устройство (регулятор).
Рисунок 1.1 Примеры структурных схем: а) – один элемент системы, б) – несколько элементов системы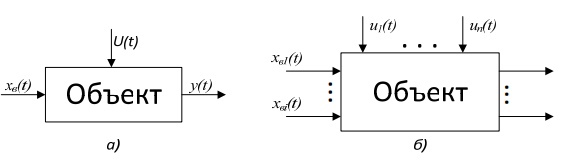 
Рисунок 1.2 Примеры изображения объектов с входными и выходными сигналами: а) – односвязный – характеризуется наличием векторов, имеющих по одной координате; б) – многосвязный – характеризуется несколькими взаимосвязанными координатами
Любой элемент системы характеризуется входной координатой (сигналом) x(t) и выходной координатой y(t), которая зависит от входного сигнала. В свою очередь входная координата может носить возмущающий и управляющий (регулирующий) характер. Возмущающее воздействие (возмущение) xB(t) вызывает отклонение управляемой (регулируемой) координаты от заданного значения. Управляющее u(t) (регулирующее xp(t)) воздействие служит для поддержания управляемой (регулируемой) координаты у(t) в соответствии с некоторым законом управления (поддержания регулируемой координаты на заданном уровне) (рис. 1.2).
Целью рассмотрения системы автоматического управления может быть решение одной из двух задач – задачи анализа системы или задачи синтеза. В первом случае дается система, включая значение параметров, и требуется определить ее свойства.
Во втором случае, наоборот, задаются свойства, которыми должна обладать система, т.е. требования к ней, и необходимо создать систему, удовлетворяющую этим требованиям. Очевидно, что задача синтеза много сложнее задачи анализа уже из-за ее неоднозначности.
Как показано на рис. 2(а) в самом общем случае на вход управляющего устройства, помимо задающего воздействия ХЗ поступает также информация о текущем состоянии объекта в виде выходной величины X и о действующем на объект возмущении F. Управляющее устройство перерабатывает получаемую информацию по определенному заложенному в нем алгоритму (закону).
В результате на его выходе возникает управляющее воздействие.
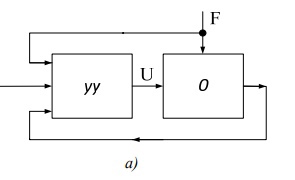
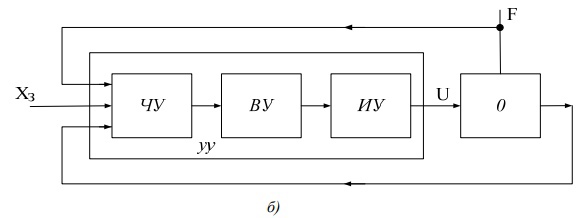Рисунок 2. Блок-схема (а ) и функциональная схема (б ) системы автоматического управления.
На рис. 2 (б) изображена функциональная схема САУ, на которой показаны основные составные части управляющего устройства: чувствительное устройство (ЧУ), вычислительное устройство (ВУ) и исполнительное устройство (ИУ).
Чувствительные устройства (измерительные устройства, датчики) служат для измерения подаваемых на управляющее устройство воздействий (сигналов) X, Х3 и F.
Вычислительное устройство реализует алгоритм работы управляющего устройства. В простейшем случае оно осуществляет простые математические операции, такие, как операция сравнения, определяющая разность Х3 – X, операции интегрирования, дифференцирования, статического нелинейного преобразования и т. п. В более сложных случаях вычислительное устройство может представлять собой цифровую вычислительную машину (ЦВМ) и даже комплекс таких машин.
Исполнительные устройства предназначены для непосредственного управления объектом, т. е. изменения его состояния в соответствии с сигналом, выдаваемым вычислительным устройством.
Помимо перечисленных выше частей, в состав управляющего устройства могут входить различные специальные устройства, например преобразователи, служащие для согласования отдельных частей системы, устройства связи и т. п.
При рассмотрении процессов в САУ важное значение имеют следующие понятия: устойчивость системы, качество процесса управления и точность управления.
Устойчивость – это свойство системы возвращаться в установившееся состояние после того, как она была выведена из этого состояния каким-либо возмущением. Замкнутые САУ, как всякие замкнутые системы, весьма склонны к потере устойчивости, что чаще всего проявляется в возникновении расходящихся колебаний (генерации). Например, такая неустойчивость системы регулирования напряжения генератора, изображенной на рис. В-2, в, выразится в возникновении колебаний напряжения генератора со все возрастающей амплитудой. Переходные процессы, показанные на рис. В-3, соответствуют устойчивой системе, поскольку отклонения напряжения со временем не возрастают, а уменьшаются, затухают. Если отбросить особые случаи, можно сказать, что устойчивость является необходимым условием работоспособности всякой САУ.
Качество процeсса управления характеризуется тем, насколько процесс управления близок к желаемому. Количественно оно определяется критериями качества, которые выбираются в соответствии с целью управления. Например, для упомянутой выше системы регулирования напряжения генератора качество может оцениваться такими критериями, как величина максимального отклонения напряжения генератора, вызванного скачком нагрузки, колебательность переходного процесса, его длительность.
Точность управления характеризуется погрешностью системы в установившихся режимах. Например, для системы регулирования напряжения генератора точность определяется величиной установившегося отклонения напряжения генератора от заданного значения по окончании переходного процесса.
КЛАССИФИКАЦИЯ СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ
Для ознакомления с основными видами систем автоматического управления и соответствующей терминологией рассмотрим классификацию САУ по ряду признаков, существенных с точки зрения теории автоматического управления.
А. Разомкнутые, замкнутые и комбинированные системы
схеме САУ, изображенной на рис.2 на управляющее устройство поступают три вида информации: информация о величине X, определяющей состояние объекта, информация о величине Х3, задающей цель управления, информация от F – возмущениях, нарушающих режим работы объекта. Однако возможны САУ, в которых используется лишь часть перечисленной информации. При этом в зависимости от видов используемой управляющим устройством информации различают два основных типа САУ – разомкнутые системы и замкнутые системы.
В разомкнутых САУ выходная величина объекта X не измеряется, т. е. нет контроля за состоянием объекта. Разомкнутыми такие системы называются потому, что вследствие этого в них отсутствует обратная связь между выходом объекта и входом управляющего устройства, при наличии которой объект и управляющее устройство образуют замкнутый контур.
Возможны разомкнутые САУ, в которых управляющее устройство измеряет только одно задающее воздействие Х3, одно возмущение F и, наконец, оба эти сигнала одновременно.
В первом варианте разомкнутой САУ управление осуществляется по задающему воздействию: поступающие извне команды Х3 приводят путем изменения управляющего воздействия U к соответствующему изменению выходной величины объекта X. Точность обеспечиваемого при этом соответствия между X и Х3 целиком определяется постоянством параметров системы и возмущений и никак не контролируется. Поэтому практически такие системы пригодны лишь при достаточно высокой стабильности указанных выше условий работы системы и невысоких требованиях к точности.
Примером системы этого типа служит разомкнутая система программного управления напряжением синхронного генератора, изображенная на рис. 3(а):
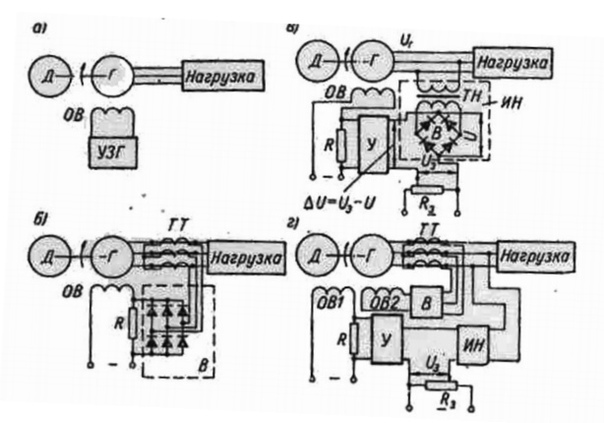Рисунок 3. Системы управления напряжением синхронного генератора: а – разомкнутая система программного управления; б – разомкнутая система компенсации влияния нагрузки; в – замкнутая система управления по отклонению; г – комбинированная система управления отклонению с компенсацией влияния нагрузки.
Объектом управления здесь является синхронный генератор Г, вращаемый с постоянной скоростью двигателем Д: Выходная величина объекта – напряжение генератора – определяется напряжением возбуждения, подаваемым на обмотку возбуждения генератора ОВ от устройства задания графика напряжения УЗГ. Последнее является управляющим устройством. Напряжение возбуждения автоматически изменяется во времени в соответствии с заложенной в УЗГ программой, обеспечивая соответствующее изменение напряжения генератора.
Система управления по задающему и возмущающему воздействиям является наиболее полным видом разомкнутой САУ. В этом случае управление объектом осуществляется в функции двух величии Х3 и F, т. е. здесь объединены оба предыдущих варианта разомкнутых систем.
Примером такой системы может быть система программного управления напряжением генератора, объединяющая схемы изображенные на рис. 3 а и б. (В этом случае в схеме рис. 3(б) напряжение питания цепи возбуждения должно подаваться от устройства задания графика напряжения УЗГ, показанного на рис. 3(а). В отличии от системы программного управления, изображенной на рис. 3(а) в новой схеме устраняется основная ошибка по напряжению, вызванная непостоянством нагрузки генератора.
В замкнутых САУ на вход управляющего устройства подаются задающее воздействие Х3 и выходная величина объекта X. Исходя из величины Х3, управляющее устройство определяет соответствующее требуемое значение X и, имея информацию о текущем значении X, обеспечивает необходимое соответствие между X и Х3 путем воздействия на объект.
В такой САУ управляющее устройство стремится ликвидировать все отклонения X от его значения, определяемого заданием Х3, независимо от причин, вызвавших эти отклонения, включая любые возмущения, внешние и внутренние помехи, а также изменения параметров системы
Как видно из рис.2, САУ такого типа представляют собой замкнутый контур, образованный объектом и управляющим устройством. При этом управляющее устройство создает обратную связь вокруг объекта, связывая его выход со входом. Замкнутые САУ называются поэтому еще системами с обратной связью или системами управления по отклонению .
Эти системы могут обеспечить принципиально неограниченную точность управления и представляют собой основной тип САУ.
Комбинированные САУ представляют собой объединение в одну систему замкнутой системы управления по отклонению и разомкнутой системы управления по внешнему воздействию. Показанная на рис. 2 схема является схемой такой комбинированной САУ.
Добавление к замкнутой системе управления разомкнутой системы компенсации влияния на выходную величину объекта какого-либо возмущения облегчает задачу замкнутой САУ и тем самым позволяет упростить ее и повысить точность управления. Лучшее качество управления в комбинированных системах объясняется тем, что в них наиболее полно используется информация об объекте и внешней ситуации.
Б. Системы автоматического регулирования – системы стабилизации, системы программного управления и следящие системы
Частным, но широко распространенным видом систем автоматического управления являются системы автоматического регулирования (САР). Системой автоматического регулирования называется САУ, задача которой заключается в поддержании выходной величины объекта X на заданном уровне ХЗ, т. е. поддержание равенства X = Х3.
В зависимости от характера задающего воздействия САР делятся на три вида: системы стабилизации, системы программного управления и следящие системы.
В системах стабилизации задающее воздействие постоянно, в системах программного управления оно изменяется по заранее заданному закону, в следящих системах оно тоже изменяется, но закон изменения заранее не известен. В последнем случае задающее воздействие поступает на систему извне и задачей системы является обеспечение слежения выходной величиной объекта за изменяющейся задающей величиной так, чтобы все время поддерживалось равенство X = Х3.
Управляющее устройство в системах автоматического регулирования называется регулятором , а выходная величина – регулируемой величиной.
Примерами систем автоматического регулирования служат системы, показанные на рис. 3, (б, в, г). Объектом регулирования здесь является синхронный генератор, регулируемой величиной – его напряжение, а обведенные пунктиром управляющие устройства – регуляторами.
В. Одномерные и многомерные системы
В зависимости от количества выходных координат объекта управления, образующих вектор выходной величины X, САУ делятся на одномерные и многомерные (двухмерные и т. д.).
Рассмотренные выше системы автоматического регулирования напряжения синхронного генератора (см. рис. 3) являются одномерными системами. Если наряду с напряжением регулировать частоту этого генератора путем воздействия на скорость вращающего его двигателя, получится двухмерная система автоматического регулирования.
Многомерные САУ (и САР), в свою очередь, делятся на системы связанного и несвязанного управления (регулирования).
Система несвязанного управления — имеет несколько управляющих устройств, каждое из которых осуществляет управление своей выходной координатой объекта. При этом все эти устройства не имеют взаимных связей. (Последнее, однако, не исключает возможности влияния управляющих устройств друг на друга через объект управления или, например, общий источник питания.)
В системе связанного управления отдельные управляющие устройства связаны друг с другом внешними связями.
Входящая в состав многомерной системы управления (как связанной, так и несвязанной) отдельная система управления называется автономной , если управляемая ею выходная координата объекта не зависит от’ значений остальных его координат, так что изменение последних не вызывает изменения этой координаты.
Г. Системы линейные и нелинейные
Линейной называется система, которая описывается линейными уравнениями. В противном случае система является нелинейной . Чтобы система была нелинейной, достаточно иметь в ее составе хотя бы одно нелинейное звено, т. е. звено, описываемое нелинейным уравнением.
Для линейных систем справедлив принцип суперпозиции. Он заключается в том, что реакция системы на любую комбинацию внешних воздействий равна сумме реакций на каждое из этих воздействий, поданных на систему порознь. Принцип суперпозиции позволяет выразить реакцию системы на любое произвольное воздействие через реакцию системы на элементарное типовое воздействие, например, в виде ступеньки. Для этого достаточно представить данное входное воздействие в виде совокупности выбранпых типовых воздействий. Благодаря принципу суперпозиции разработана общая теория линейных систем автоматического управления, описываемых линейными дифференциальными уравнениями любого порядка.
К нелинейным системам принцип суперпозиции не применим. Нет и общей теории нелинейных дифференциальных уравнений, на основе которой могла бы быть создана общая теория нелинейных систем автоматического управления. Существует лишь ряд частных методов для решения некоторых видов нелинейных уравнений невысокого порядка. Вместе с тем, если не ограничивать диапазона изменения входных воздействий, то все реальные системы автоматического управления оказываются нелинейными. Трудность исследования нелинейных систем заставляет упрощать их описание. Желательным пределом такого упрощения является приближенное описание их линейными -уравнениями, хотя бы в некоторых из интересующих нас режимов. Это называется линеаризацией нелинейных систем. В тех случаях, когда линеаризация невозможна, прибегают к приближенным методам исследования нелинейных систем с учетом их нелинейностей.
Д. Системы стационарные и нестационарные
Стационарной называется система, все параметры которой не изменяются во времени. Нестационарная система – это система с переменными параметрами. При математическом описании нестационарной системы это проявляется в том, что некоторые коэффициенты дифференциального уравнения системы являются функциями времени.
В соответствии с данным определением, в отличие от нестационарной системы, реакция стационарной системы на одно и то же воздействие не зависит от момента приложения этого воздействия.
Е. Системы непрерывного и дискретного действия
САУ бывают непрерывного или дискретного действия в зависимости от характера действия составляющих систему звеньев.
Система непрерывного действия, или, короче, непрерывная система , состоит только из звеньев непрерывного действия, т. е. звеньев, выходная величина которых изменяется плавно при плавном изменении входной величины.
Система дискретного действия, или дискретная система, – это система, содержащая хотя бы одно звено дискретного действия. Звеном дискретного действия называется звено, выходная величина которого изменяется дискретно, т. е. скачками, даже при плавном изменении входной величины. (Скачки выходной величины могут происходить либо при прохождении входной величиной определенных пороговых значений – звено релейного, действия, либо через определенный интервал времени – звено импульсного действия.)
Ж. Адаптивные и неадаптивные системы
Адаптивные, или самоприспосаливающиеся, системы обладают способностью приспосабливаться к изменению внешних условий работы, а также улучшать свою работу по мере накопления опыта. Неадаптивные, или, как их еще называют, обыкновенные, системы такой способностью не обладают. Они имеют постоянную настройку. Если вследствие какого-либо изменения условий работы обыкновенной системы ее настройку требуется изменить для того, чтобы сохранить заданное качество управления (например, точность, быстродействие), эту перенастройку должен сделать человек. В случае адаптивной системы это осуществляется автоматически самим управляющим устройством системы.
Область применения адаптивных САУ – это управление объектами, свойства или условия работы которых недостаточно известны или существенно непостоянны. В этих условиях обыкновенная, неадаптивная, система либо будет работать неудовлетворительно, либо потребует постоянного надзора.
Источник: m.vk.com
