Распознавание эмоций с использованием нейронной сети
Для обучения будем использовать часть датасета CREMA, которая представляет собой набор аудиофайлов, на которых актеры с различными эмоциями произносят 12 фраз. Подробное описание данных можно найти здесь.
Исходный набор данных:

Прежде всего, необходимо определить какая эмоция характеризует аудиофайл (явное указание на эмоцию есть в имени файла). Запишем результаты в датафрейм:

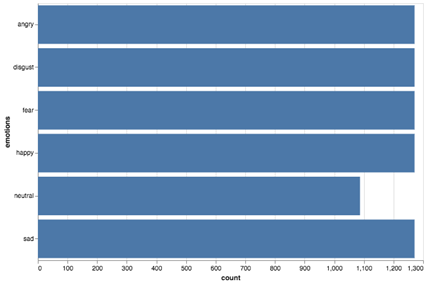
Всего в наборе представлено 6 различных эмоций, при этом данные сбалансированы.
Для анализа и извлечения данных из аудиофайлов будем использовать библиотеку librosa. Для примера посмотрим на волны «счастья» и «злости».
def wave(data, sr, e): plt.figure(figsize=(10, 3)) plt.title(‘Waveplot for {}’.format(e), size=15) librosa.display.waveplot(data, sr=sr) plt.show() 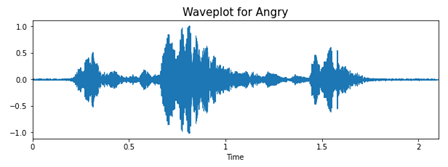
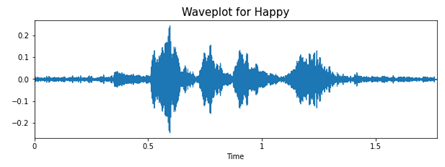
При гневе вся фраза как будто бы произносится на одном дыхании, с большим напором в начале, это отчетливо видно на графике. Если посмотреть на график «счастья», то можно заметить, что фраза произносится протяжнее, равномернее. Видно, что на записях присутствуют небольшие шумы. Именно изменение интонации и тембра голоса поможет нам классифицировать эмоции, представленные на аудиозаписях.
Данные, полученные из аудио, не могут быть использованы для обучения модели напрямую, поэтому преобразуем их в подходящий формат. Одними из лучших инструментов для извлечения информации из звуковых сигналов являются MFCC (Мел-кепстральные коэффициенты). Коэффициенты описывают форму спектральной огибающей сигнала. Пройдемся по записям. Считаем их, отбросив 0,15 секунды в начале, а длину записей ограничим 3 секундами. В качестве признаков будем использовать средние значения mfcc.
df_1 = pd.DataFrame(columns=[‘feature’]) i=0 for index,path in enumerate(df.path): X, sample_rate = librosa.load(path, duration=3, offset=0.15) sample_rate = np.array(sample_rate) mfccs = np.mean(librosa.feature.mfcc(y=X, sr=sample_rate, n_mfcc=20), axis=0) df_1.loc[i] = [mfccs] i=i+1
Результаты извлечения признаков:

Итак, задача свелась к многоклассовой классификации. Преобразуем целевую переменную для дальнейшего использования, а также разделим данные на train и test соответственно.
y= pd.get_dummies(df_1.path) tr_x, test_x, tr_y, test_y= train_test_split( df_1.drop([‘emotions’,’path’], axis=1), y, test_size=0.3, random_state=42)
Построим классическую одномерную сверточную нейронную сеть. Добавим Dropout слои, чтобы избежать переобучения, а также слои пуллинга (MaxPooling1D) для уменьшения размерности.
in_node = Input( shape = (130,1)) out_node = Conv1D (128,4, padding = ‘same’, activation = ‘relu’)(in_node) out_node=Dropout(0.15)(out_node) out_node = MaxPooling1D(pool_size=(4))(out_node) out_node=Conv1D(64,4, padding=’same’, activation = ‘relu’)(out_node) out_node=Dropout(0.15)(out_node) out_node = MaxPooling1D(pool_size=(4))(out_node) out_node=Conv1D(32,4, padding=’same’, activation = ‘relu’)(out_node) out_node=Flatten()(out_node) out_node=Dense(6, activation=’sigmoid’)(out_node) mod=Model(inputs = in_node, outputs = out_node) mod.compile(loss = ‘categorical_crossentropy’, optimizer = ‘adam’, metrics=[‘accuracy’]) mod.fit(tr_x,tr_y, epochs=70)
Построим график изменения точность в процессе обучения.
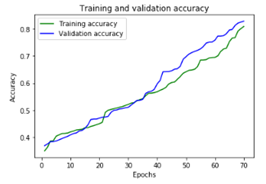
Результаты на тестовой выборке:
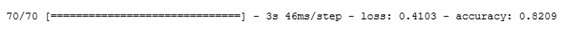
Получился довольно неплохой результат. В данном наборе представлены записи и мужских, и женских голосов, а они различаются по тембру и высоте голоса, можно классифицировать их по отдельности. Также можно извлекать другие характеристики сигнала (скорость пересечения нуля, спектральный центроид). Внося некоторые изменения в исходные данные (добавить шумы, сдвиги, увеличить скорость произношения), можно генерировать новые данные, которые помогут сделать модель более устойчивой к возмущениям и повысить её обобщающую способность.
Источник: newtechaudit.ru