После 32 лет исследований загадка 9-го числа Дедекинда была решена благодаря суперкомпьютеру
После 32 лет исследований ученые решили загадку девятого числа Дедекинда (с 23 цифрами), сложную математическую проблему, с помощью суперкомпьютера Noctua. Это открытие, для которого потребовались передовые вычислительные методы, проливает свет на до сих пор неизученный аспект монотонных булевых функций. Это демонстрирует потенциал суперкомпьютеров для решения сложных математических задач и открывает путь к новым исследованиям в этой области.
Некоторые математические загадки, управляющие нашей реальностью, такие как золотое сечение, продолжают удивлять исследователей своей сложностью. Среди них некоторые математические сущности вызывают интерес с момента их открытия Рихардом Дедекиндом в конце 19 века. Некоторые сложные числовые задачи касаются «монотонных булевых функций», которые долгое время хранили свои секреты — восемь из них были решены лишь недавно. Однако проблема «девятого числа Дедекинда» остается неуловимой уже более трех десятилетий, представляя собой серьезную проблему для математического сообщества.
Недавно группе исследователей из Университета Падерборна и университета Лёвена удалось разгадать эту тайну, в частности, благодаря инновационному использованию суперкомпьютера Noctua. Это достижение, потребовавшее годы интенсивных исследований и расчетов, знаменует собой значительный прогресс в области математики и открывает новые перспективы для решения сложных проблем. На данный момент отчета об исследовании нет, но он должен быть представлен в сентябре на международном семинаре по булевым функциям и их приложениям (BFA), который пройдет в Норвегии.
Числа Дедекинда — сложное понятие
Числа Дедекинда — это особые математические единицы, целые числа, которые играют центральную роль в изучении монотонных булевых функций. Булевы функции — это форма математической логики, которая оперирует двоичными значениями, то есть значениями, которые могут принимать два различных состояния. Эти состояния могут быть представлены различными способами: истина и ложь или 0 и 1. В контексте чисел Дедекинда эти булевы функции используются для определения выхода из набора двоичных входов.
Монотонные булевы функции являются их подкатегорией. У них есть особенность: они устроены таким образом, что замена 0 на 1 на входе приводит только к изменению выхода с 0 на 1, но не наоборот. Другими словами, эти функции «монотонны» в том смысле, что они не «возвращаются назад»: после того, как значение было изменено с 0 на 1, оно не может быть изменено в обратном направлении.
Леннарт Ван Хиртум, ведущий автор исследования, объясняет в пресс-релизе: «В принципе, монотонную булеву функцию в двух, трех или n измерениях можно представить как игру с n-мерным кубиком. Вы балансируете кубик на одном углу, затем окрашиваете каждый из оставшихся углов в белый или красный цвет. Есть только одно правило: никогда не кладите белый угол на красный. Это создает своего рода красно-белое вертикальное пересечение. Цель игры — подсчитать количество различных возможностей. Число возможностей известно как число Дедекинда. Даже если так не кажется, в процессе игры числа быстро становятся гигантскими: 8-е число Дедекинда состоит уже из 23 цифр».
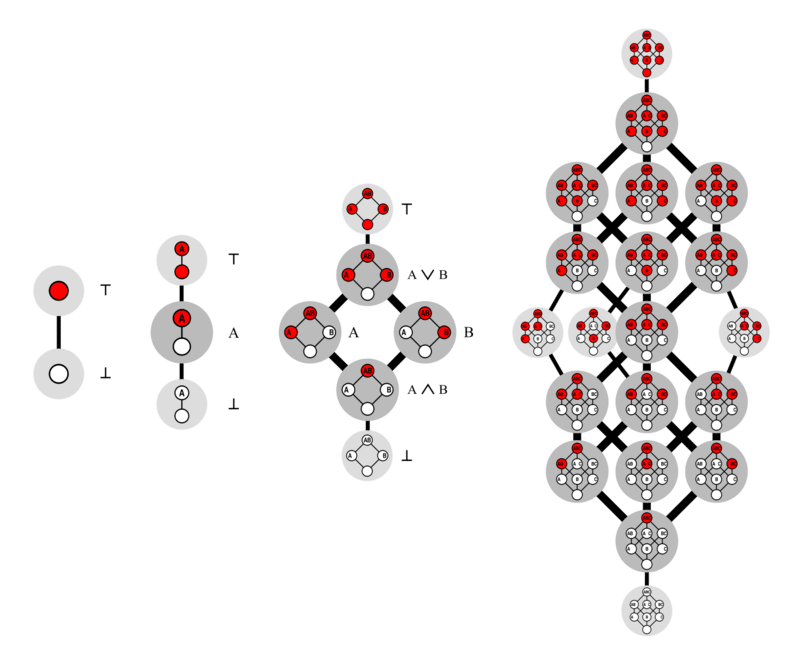На рисунке показаны все возможные разрезы для размеров 0, 1, 2 и 3. Количество этих 2D, 3D, -N-мерных цветных разрезов, которые могут быть образованы, определяется как число Дедекинда.
Эти функции играют важнейшую роль во многих областях математики и информатики, особенно при изучении структур данных, алгоритмов и теории графов.
Решение математической загадки
Открытие девятого числа Дедекинда, или D(9), стало возможным благодаря использованию передовых методов вычислений и мощности суперкомпьютера Noctua. Чтобы решить эту проблему, исследователи использовали методику, известную как формула коэффициента P.
Эта формула предоставляет метод вычисления чисел Дедекинда не путем подсчета, а путем выполнения очень большой суммы. Это позволило расшифровать D(8) всего за восемь минут на обычном ноутбуке. Однако то, что занимает восемь минут для D(8), превращается в сотни тысяч лет для D(9), даже при использовании большого суперкомпьютера.
Чтобы добиться этого, исследователям пришлось прибегнуть к высокоспециализированным параллельным арифметическим устройствам, называемым FPGA (Field Programmable Gate Arrays). Ван Хиртум разработал первоначальный прототип аппаратного обеспечения, предназначенного для ускорения определенных типов компьютерных вычислений. Затем исследователи обратились к суперкомпьютеру Noctua 2 в Падерборнском центре параллельных вычислений (PC2) при университете Падерборна, который располагает одной из самых мощных систем FPGA в мире.
Важное открытие
После нескольких лет разработки программа проработала на суперкомпьютере около пяти месяцев. А 8 марта 2023 года ученые обнаружили девятое число Дедекинда: 286386577668298411128469151667598498812366. Это открытие подчеркивает впечатляющую мощь суперкомпьютеров и передовых методов вычислений.
Эти машины могут выполнять миллиарды вычислений в секунду, используя огромные объемы данных, что делает их незаменимыми для решения сложных математических задач, таких как девятое число Дедекинда. Передовые методы вычислений позволяют структурировать и оптимизировать эти вычисления, чтобы максимально использовать возможности этих суперкомпьютеров.
Но помимо демонстрации возможностей суперкомпьютеров и передовых методов вычислений, это открытие также прокладывает путь для новых исследований и открытий в области математики. Решение девятого числа Дедекинда может привести к лучшему пониманию монотонных булевых функций и их применению в различных областях, от информатики до логики.
Источник: new-science.ru
